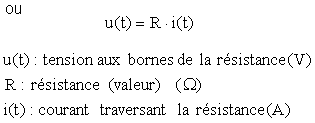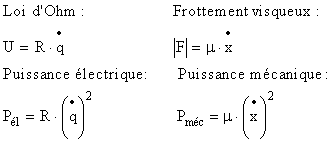LE POTENTIOMETRE

 

 

Les Résistances Ajustables

1.1.Descriptions

La résistance ( Résistor) est l'élément le plus simple, très utilisé en électronique.
C'est un composant dit passif , il conduit l'électricité avec un effet résistif .
Il est bidirectionnel , il n' y a pas de sens obligatoire du passage du courant .

Lorsqu'il est nécessaire de faire varier la valeur de la résistance, on utilise un système à curseur qui frotte sur celle-ci, faisant intervenir ainsi dans le circuit une portion variable de la résistance totale ; on réalise de la sorte un potentiomètre, qui peut être de type rotatif, à forme circulaire, ou de type linéaire. La piste rotative ou linéaire est en bakélite recouverte de carbone pour les modèles les moins chères.

Dans sa forme miniature ces résistances se présentent sous la forme d'un petit boîtier muni de trois pattes à souder sur le circuit imprimé: les résitances ajustables ; il existe une grande variété de modèles à piste de carbone ou cermet , capotés ou non verticaux ou horizontaux. Dans tout les cas la patte centrale est connecté au curseur comme le montre le symbole.

1.2.Symboles

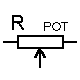ou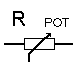

1.2. Unités

L'unité de mesure de résistance est l'Ohm :

La valeur d'une résistance R s'échelonne d'une fraction d'ohm à quelques mégohms :

1.3. Formules

1.3.1.Résistance statique :

Le concept de résistance est défini comme le rapport de la tension sur le courant :

La valeur d'une résistance R s'échelonne d'une fraction d'ohm à quelques mégohms .
La tension aux bornes de la résistance u en volt.
l' intensité du courant i en ampères.

1 ohm ; 10 ohms ; 100 Ohms

1000 ohms = 1 Kohms = 1K (1 kilo ohms )

1000000 ohms = 1000 Kohms = 1 Mohms = 1M ( 1 mégohm )

1.3.2.Loi d'ohm

La loi d'Ohm se traduit par la relation 

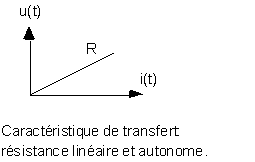
R étant la résistance exprimée en ohms qui caractérise ce conducteur , et certains  matériaux ont un comportement linéaire :

1.3.3.Effet résistif :

Il convient de noter que la dégradation d'énergie en forme thermique est un phénomène général en physique, phénomène décrit par la thermodynamique. En électricité, si on place une tension aux bornes d'un conducteur, il advient un courant. La dissipation d'énergie se manifeste par un échauffement et une chute de potentiel le long du conducteur ; il y a conversion d'énergie électrostatique (contenue dans le générateur par exemple) en énergie thermique (échauffement par effet Joules).

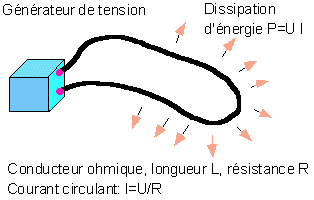
Lorsqu'on branche un conducteur à une tension donnée, il résulte un courant, dont l'intensité dépend de la résistance du conducteur à son passage.

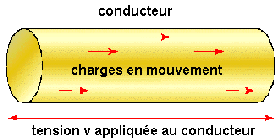
Le courant I mesuré en ampères est égal à la quantité d'électricité mesurée en coulombs qui passe par seconde dans le conducteur.

La résistance d?un corps dépend de sa nature par sa résistivité (qui n?est autre que sa faculté à s?opposer au passage des électrons) et de ses dimensions (longueur et section). La relation donnant la résistance R d?un cylindre de section constante (mais de forme quelconque) .

La résistivité ( ) se dit ro s' exprime en ohms par mètres .

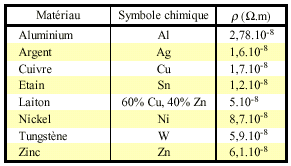
La formule  R = L / S 

R en Ohms , en Ohms x mètres , L longueur du matériau en mètre , S la section en m²

La résistivité dépend elle-même de la température (T) du matériau.

1.3.4. Loi de joule :

La loi de Joule donne la valeur de l'énergie thermique W dégagée durant le temps t dans le conducteur par la relation

W = RI²t en Watts

Avec 1 résistance ajustable :

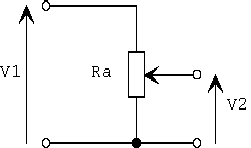Ici V2 peut être ajusté entre 0 et V1.

V2 = k*V1 avec k réel entre 0 et 1

Notez que ces formules sont applicables seulement si la charge en sortie consomme très peu de courant. Sinon, la résistance de charge se met en parallèle avec R2, et donc la résistance du bas devient R2 // Rcharge, soit (R2 * Rcharge) / (R2 + Rcharge).

1.4.Variantes

Cet élément peut servir de résistance variable manuellement, si l'on connecte deux des trois bornes ensemble.

Le symbole est aussi parfois utilisé pour exprimer que dans un circuit, la valeur de la résistance est commandée.

Ont dit aussi résistance ajustable lorsqu' il s agit de potentiomètre miniature pour être soudés directement sur un circuit, il en existe à 1 tours ou multi tours ( 15 , 25 ) . Le réglage s'effectue soit horizontalement ou verticalement .Les valeurs courantes vont de 47 ohm à 10 Mohm selon l' échelonnement de la série E3 ( 10 - 22 - 47 ).

Extrait de fiche technique d'un potentiomètre ajustable miniature pour circuit ( réglage vertical ) :

Dans sa forme boîtier, le potentiomètre peut être de type rotatif, à forme circulaire, ou de type linéaire à glissière. De plus un nouveau critère , la loi de variation peut être Linéaire ( lin A ) ou logarithmique ( log B ).

Modèle rotatif

et modèle linéaire à glissière

Les valeurs sont celles de la série E3 ( 10 - 22 - 47 ) de 100 ohms à 1 Mohm .Le trou de perçage pour la fixation ou dimension du canon est de 10 mm avec un axe de diamètre 6 mm pour le bouton en général .Il existe des potentiomètres double pour les applications audio stéréo et aussi avec interrupteur .Les pattes sont soit à souder ou déportées (sortie sur cosses avec un trou permettant un liaison filaire ).

Autres exemples de composants résistif

1.4.1.Les Photo résistances dont la valeur de la résistance dépend de l'éclairement et sont constituées d'inclusions de sulfure de cadmium dans du plastique.

1.4.2.Les Thermistances dont la valeur de la résistance dépend de la température.

1.4.3.Les Varistances (en anglais voltage dépendent resistor), dont la valeur de la résistance est fonction de la tension appliquée.

1.5. Utilisations

Les résistances servent dans de nombreuses applications :

Elle permettent de diminuer l' intensité dans un circuit .Par exemple pour alimenter une LED

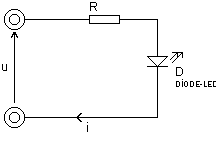
ou dans un circuit à transistor pour limiter le courant :

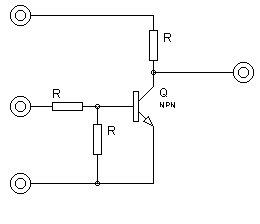
etc...

1.6. Mesure de Résistance

Il est possible de mesurer la valeur des résistances avec notre multimètre , c' est la fonction Ohmmètre .

Important : Toute mesure de résistance doit se faire hors tension , il faut couper l' alimentation et si la résistance se trouve sur un circuit il faut dessouder une patte pour la mesure , afin de ne pas mesurer les résistances qui pourraient se trouver en parallèles .

2.Composition

En électronique, elles ne sont appelées à dissiper que des puissances très faibles, au maximum de l'ordre du watt .Les puissances les plus utilisées étant les résistances de 1/4 W = 0,25 W .

C'est pourquoi on fait appel à un matériau à base de carbone, en forme de bâtonnet, et parcouru par le courant soit dans sa masse, soit dans une couche mince de sa surface, ce qui limite alors le " bruit " ou " souffle " dans les circuits.

Les résistances agglomérées sont formées d?un mélange de carbone, de matière isolante et de liant (par exemple de la bakélite.). Le pourcentage de carbone détermine la valeur de la résistance. Les caractéristiques obtenues sont très moyennes, mais la fiabilité ainsi que le faible coût de ces résistances en faisait des composants couramment employés dans les montages électroniques .Maintenant elles sont remplacées par les résistances à couche de carbone .

vue de l' intérieur d' une résistance agglomérée

Les résistances à couches de carbone se font par pyrolyse en atmosphère d?hydrocarbure (méthane, butane ou benzène) et d?argon. le carbone se dépose sur de petits bâtons  isolant servant de support , ensuite on fixe aux extrémités des broches de connexion .

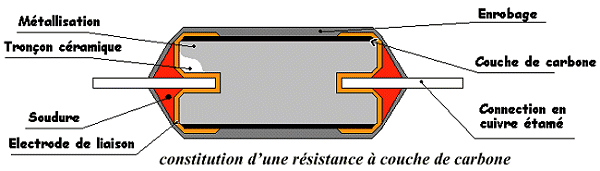
La valeur de la résistance est obtenue en retirant une partie de la couche résistive en spirale .

Les résistances à couches métallique , l?élément résistant est obtenu par la pose d'une couche d'env. 0,1mm d?un alliage sur un substrat en céramique ou en quartz.. Ce type de résistances a un petit coefficient de température.

Les résistances à feuilles métalliques (de quelques ohms à quelques méga ohms) sont des résistances très précises, constituées d?une feuille en alliage (souvent du nickel-chrome) fixée sur un substrat isolant.

La dimension augmente en fonction de la puissance dissipé le diamètre est d'environ de 6 mm pour 3 W .Pour des puissances de 5 à 11 W ont utilise alors du fil résistif bobinées .

Les résistances bobinées (de quelques ohms à quelques milliers d?ohms) sont constituées d?un fil en alliage (nickel-chrome ou cuivre-nickel pour des résistances de haute précision à faible coefficient de température) enroulé sur un support isolant en céramique ou en matière plastique puis elles sont moulées , laquées ou vitrifiées.

Les résistances miniature de surface sont faites sur un substrat en céramique de petite dimension :

versions rondes

versions plates

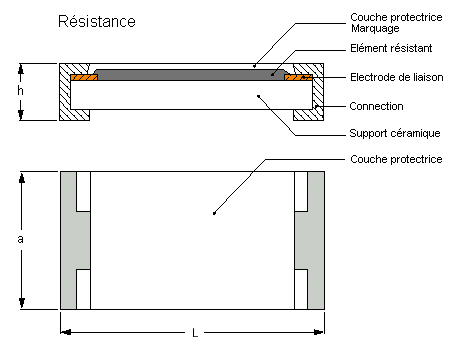
les résistances à couches épaisses (> 1 méga ohm) sont faites d?une pâte de verres fusibles et de métaux nobles déposée (quelques dizaines de µm) par sérigraphie sur un support d?alumine, puis cuite à haute température.

2.1.Formules +

2.1.1.La résistance : phénomène physique

Le phénomène physique de résistivité correspond à la résistance qu'offre l'élément au passage du courant. On écrit :

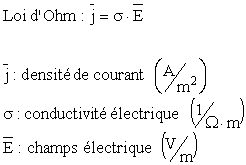
C'est une expression de la dissipation thermique (effet Joule) ; du point de vue du circuit, la résistance ne stocke pas d'énergie, mais la dissipe. La puissance instantanée vaut :

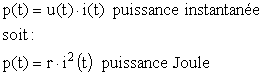
2.1.2.Résistance dynamique :


La résistance dynamique est définie comme le rapport des accroissements de courant sur ceux de tension, à un point de fonctionnement donné

.

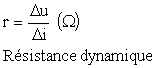Par exemple, dans le cas de la caractéristique courant-tension d'un dipôle non linéaire comme la diode, on définit sa résistance dynamique ainsi :

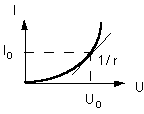
2.1.3.Résistance d'une tige conductrice

2.1.4.Linéarité et autonomie d'une résistance

Remarquons encore qu'une résistance n'est pas forcément linéaire ni forcement autonome (indépendante du temps) : lorsqu'on modélise un capteur ou un effet physique, à peu près tout peut arriver ! Il existe par exemple des résistances dont la valeur varie fortement avec la température ambiante (thermistances) ; elles peuvent être utilisées comme détecteurs ou capteurs de température.

Pour un conducteur normal, on peut utiliser une approximation linéaire en la température, si le modèle autonome est insuffisant :

2.1.5. Analogie mécanique de la résistance

En mécanique, le travail de forces de frottement représente une dissipation d'énergie du système considéré. Une de leur modélisation correspond aux forces dites de frottement visqueux, où leur intensité est proportionnelle à la vitesse de déplacement. Si on écrit la loi d'Ohm en terme de charge et de tension, on observe une similitude :

Il est clair que ni la relation courant-tension dans une résistance n'est toujours aussi simple, ni les forces de frottement toujours visqueuses et linéaires. Il s'agit en fait d'une rationalisation technique : on construit des systèmes technologiques auxquels on impose cette simplicité dans des limites de fonctionnement. Par exemple, la valeur de la résistance dépend de la température de cette dernière : elle augmente avec la température. Alors on s'arrange pour écouler la chaleur et ainsi maintenir les systèmes dans leurs plages de fonctionnement.

 

Exemple d'application en classe de 6ème: le porte clé lumineux